The Triangle of Velocities

The Navigation Computer: The Triangle of Velocities

Accordingly, we have to take account of this movement of air when we navigate and this problem is solved by constructing a vector triangle of velocities. The components are always the same:

The Air Vector: The Air Vector consists of Heading and True Airspeed (TAS). TAS is the true (not indicated) speed of the aircraft through the air, and it is the speed that the aircraft would travel over the ground if there were no wind. The Air Vector is always drawn with one direction arrow.

The Wind Vector: The Wind Vector consists of Wind Direction and Wind Speed. Wind direction is always given in terms of the direction that the wind has come from, not where it is blowing to. Thus a wind vector like this:

indicates a wind direction of 330°(T), not 150°(T). (This does actually correspond to the way that we normally discuss wind direction in everyday speech. A South wind is warm because it has blown up from Morocco, a West wind is warm and wet because it has blown across the Atlantic and over Ireland, etc.). The Wind Vector is always drawn with 3 direction arrows.

The Ground Vector. The Ground Vector is drawn by joining up the Air Vector and the Wind Vector. The resultant vector is Track and Ground Speed. The Ground Vector is always drawn with 2 direction arrows.

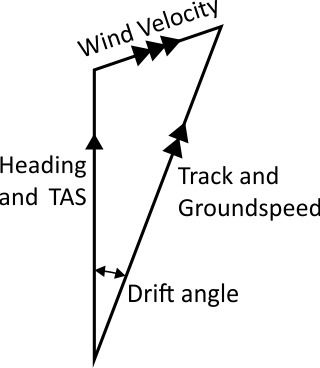
This is a diagram of the Triangle of Velocities. In practice, pilots do not normally draw it out to scale on graph paper, but solve it using an analogue navigation computer. However, as we are just about to find out, the Navigation Computer is merely a device for quickly producing a scale drawing and is actually drawing the Triangle of Velocities for you.

Next: A Practical Example