The Navigation Computer: Rates and Ratios
Let us reinforce the division process by doing another example. Placing it into an aviation related situation:-.
The average rate of climb of a particular aircraft is given as 700 feet per minute. How long will it take to climb from 3000 to 20000 feet?
The aircraft is to climb through 17000 feet at 700 feet per minute. Straightforward division of 17000 by 700 will determine the number of minutes for the climb.
What is the rough order of magnitude?
700 feet in one minute so ...
7000 feet in ten minutes, and ...
14000 feet in twenty minutes; therefore ...
17000 feet in a few more minutes than twenty ...
Alternatively, 700 fpm is not too far from 1000 fpm. So the sum is approximately 17000 / 1000, which will be a bit more than 17, i.e. somewhere in the low twenties.
Hold the computer with the 17000 (shown as 17) of the outer scale at the top.
Rotate the disc to bring the 700 (shown as 7) of the inner scale immediately opposite the outer scale 17.
Turn the instrument the shortest way (clockwise in this case) to bring 10 of the inner scale to the top.
Opposite this ‘10’ read off from the outer scale the answer digits 243.
Which leads us to a final answer of 24.3 minutes.
You may prefer a slightly different approach to this type of problem, solving in terms of proportion rather than division. Restating the problem we have:-
Aircraft climbs 700 feet in one minute.
It will climb 17000 feet in ‘t’ minutes (where ‘t’ is the answer we wish to discover).
This can be written as:-
700 / 1 = 17000 / t
Now if you arrange this equation on your circular slide rule with the numerators 700 and 17000 on the outer scale set respectively above the denominators 1 and ‘t’ on the inner scale, the problem is solved.
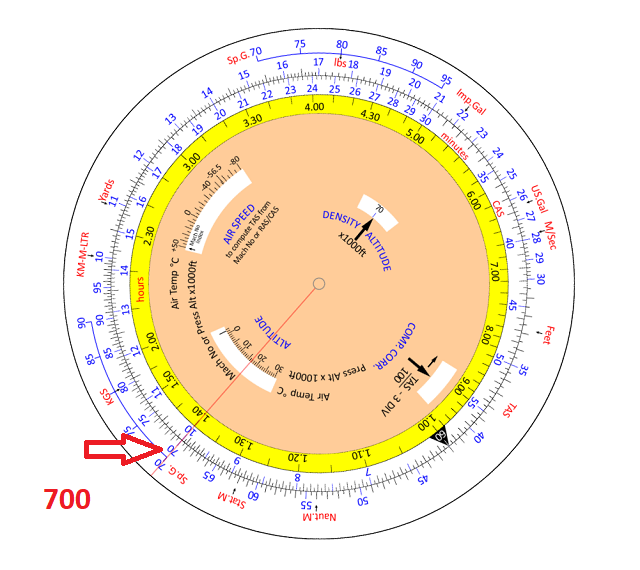
As shown in Figure 6, align the 700 (shown as 70) of the outer scale exactly over the 1 (shown as 10) on the inner scale. This sets up the left hand side of the equation.
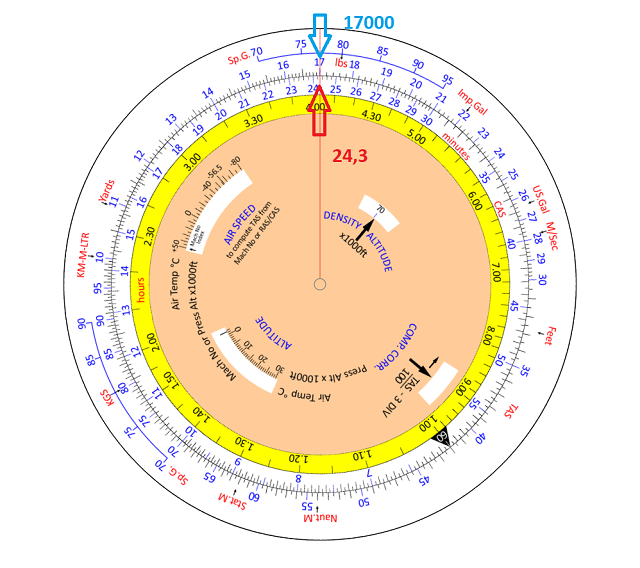
Turn the instrument clockwise and look for the right hand side of the equation. Look for 17000 (shown as 17) on the outer scale.
Immediately under it, read off 24.3 from the inner scale.
This is the same answer that we had before. If you solve the problem in this manner, you still have to perform a rough mental calculation, as before, to position the decimal point correctly.
This proportioning, or ratio, technique is important. It is the basis of all distance, speed and time calculations and of fuel consumption calculations.
© 2022 terms of use privacy policy