Slide Rule Theory

The Navigation Computer: Slide Rule Theory

It is easier to learn how to use the Navigation Computer if you understand the theory behind it rather than simply learning how to do the operations parrot-fashion. The advent of digital calculators over the last 30 years has meant that few students have experience of the oldfashioned engineer’s slide rule. The Navigation Computer uses the same slide rule theory except that instead of the scales being presented on a straight ruler they are on 2 circular discs.

We will start this explanation by imagining that we have a problem of addition, not multiplication.

Imagine that you had to add two numbers, but you had never learnt how to do simple addition. One way to solve the problem would be to use two rulers.

Suppose you had to add 3 + 2. Put the zero of the top ruler against the ‘3’ on the bottom. Now look down from the ‘2’ on the top ruler to read off the ‘5’ on the bottom.

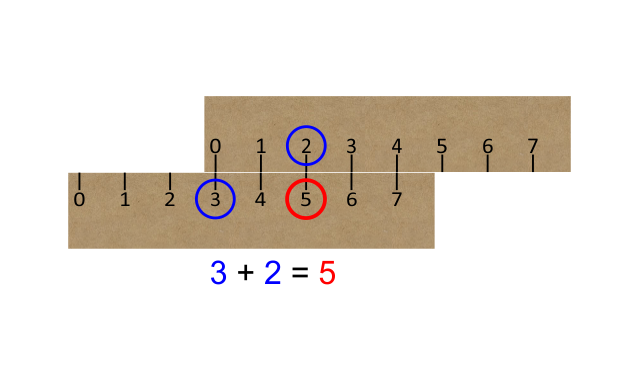
In addition, note that with just one alignment of the ruler you can also read off the answer to the sum:-

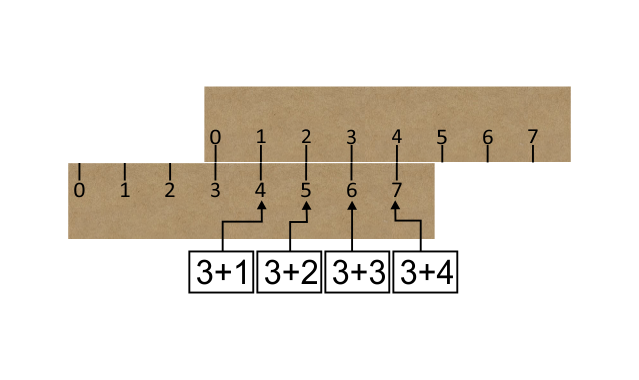
3 + any other number = ?

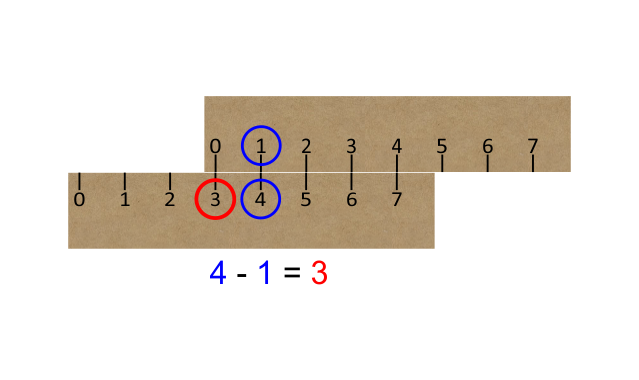
Note: You can also subtract. By aligning ‘4’ on the bottom ruler with ‘1’ on the top ruler and then looking back to the zero on the top ruler, you can read off the answer ‘3’

Now, keeping that at the back of our mind, let us deal with a different problem. Suppose you had to multiply 4 × 8, but had never learnt to do simple multiplication. Another way to tackle this problem would be to treat it as 2² × 2³.

This is the same as saying (2 × 2) × (2 × 2 × 2), which is 2 × 2 × 2 × 2 × 2.

So 2² × 2³ = 2⁵

In other words, to multiply 2 numbers expressed as powers of the same base, you add their indices.

Now, if we put our numbers on a ruler again, but on a logarithmic, not a linear scale, the length of the rulers is scaled in proportion to their indices.

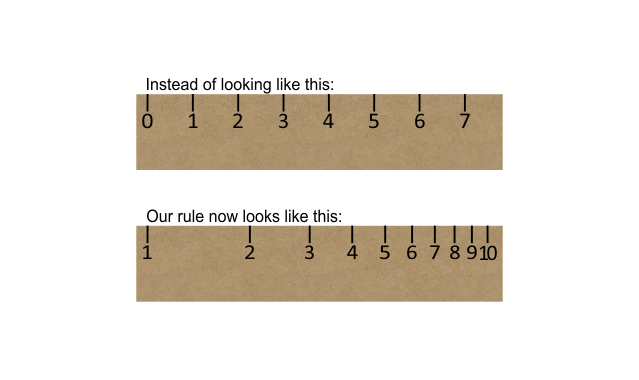
We can now use our rulers for multiplying and dividing instead of adding and subtracting. This is much more useful.

For example, in order to multiply by 2, we align the ‘1’ on the top scale with the ‘2’ on the bottom scale.

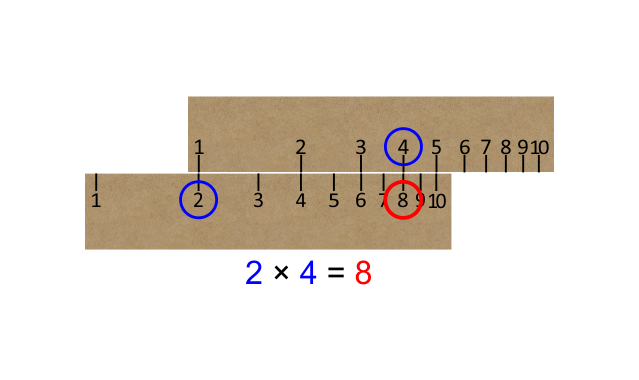
Then, by simply reading off the top scale at any point we can find that number multiplied by 2 on the bottom scale.

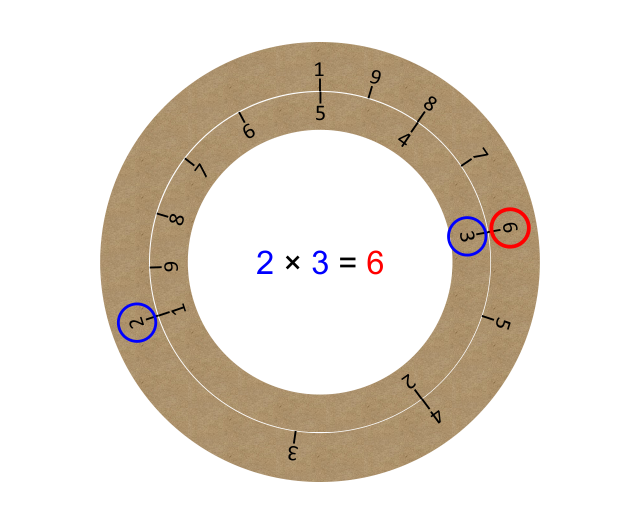
This works for any number. Suppose we now want to multiply by 3. All we do is align the ‘3’ on the bottom scale with the ‘1’ on the top scale as in Figure below. We have now set the scales in the ratio 3:1. We do not need a different scale for each number. The same 2 scales do all numbers.

Now ‘1’ is aligned with ‘3’, ‘2’ is aligned with ‘6’, ‘3’ is aligned with ‘9’, and so on.

Note that it works with the positions of the two scales reversed. We can have our 2 scales like this:

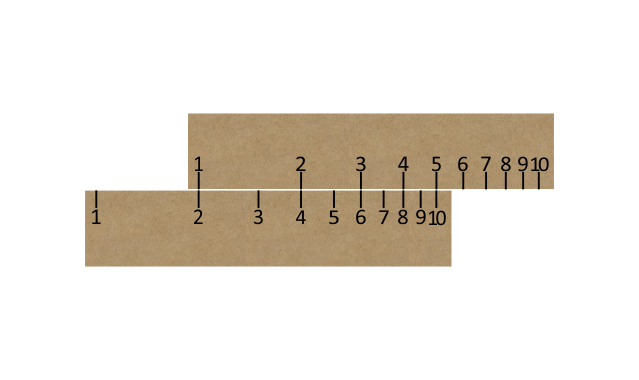
Or like this:

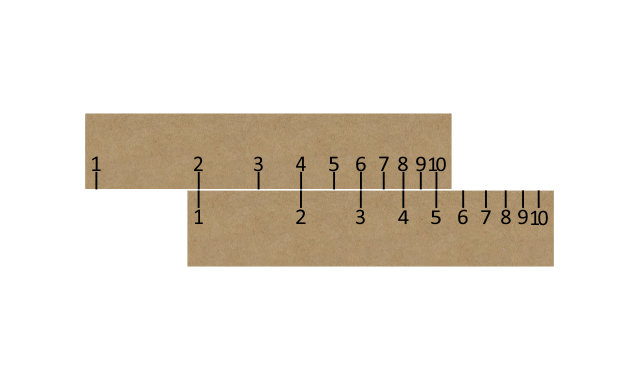
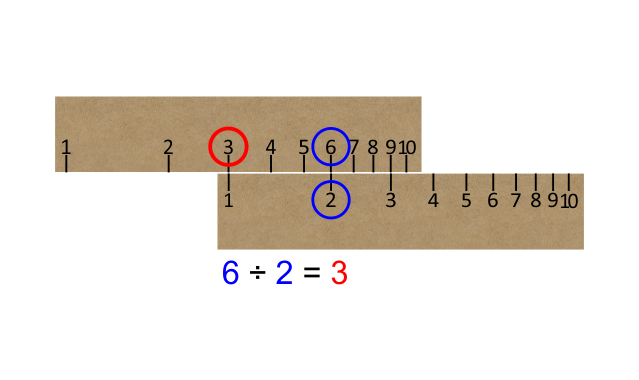
Note: We can use it for dividing as well as multiplying, in the same way that we could use the linear scale for subtracting as well as adding.

When set up like this, we can divide 6 (top scale) by 2 (bottom scale), and read off the answer ‘3’.

The Navigation Computer turns our straight slide rule into a circular one, as follows:-

Next: Multiplication